Here is the data folks submitted to the Google Form in class today. I sorted according to each variable so you can easily figure out mean, median and mode etc. Use this data to complete the handout you received in class on Friday. THEN... read below to learn how to complete this assignment on in a comment on this blog post. I wonder why some folks are missing from the data...
 |
NOTE: There are two people who listed their height as 63 and 64 cm. Since nobody in our class is around two feet tall, I assume those are errors. Before I graphed the data I added a "1" to each so they became 163 and 164 cm. In psych or any type of research, our conclusions are only as good as the data we use to form them. How we deal with errors in data collection is an important issue.
I strongly suggest you write the comment in Word or another program and then copy and paste it into the comment section below. This way, if the comment doesn't go through or is accidentally deleted you'll have a record of your work. Please also remember that I have to approve all comments, so it may take a while for it to show up on the blog. You don't need to resubmit it over and over.
Click on graphs to enlarge.
What can we see from the above scatter plot of hair length vs. height? Is there a correlation? How strong is it? If so, is it positive or negative; strong or weak?
Graph 2
Height vs. Shoe Size
Height vs. Shoe Size
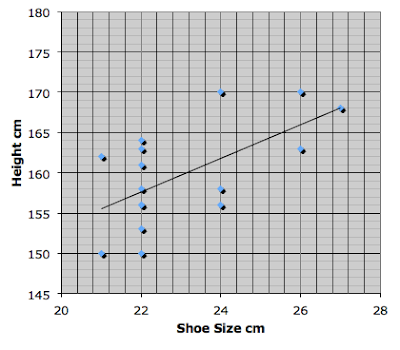 |
| Height vs. Shoe Size Correlation Coefficient 0.61 |
Above is the data we collected about our shoe sizes vs our heights. Can you see a relationship? Is there a correlation? If so, is it positive or negative? How strong is it? Does shoe size cause height to change? Does height cause shoe size to change? Why are some values so common?
Graph 3
Shoe Size vs. Hair Length
 |
| Shoe Size vs. Hair Length Correlation Coefficient -0.82 |
Finally, the above graph shows the relationship between shoe size and hair length. Is there a correlation? If so, is it positive or negative? How strong is it? Are the points clustered in an interesting way? What third variable which is not shown on any of the graphs might be causing the relationship between shoe size and hair length? Does correlation imply causation? Why or why not?
And a video about ice cream and polio...
Hank on Research Methods
And... more about the Standard Deviation
While you don't need to calculate the Standard Deviation on the AP exam, this video explains how to do it. You may find it helpful to go through the math to help you understand the concept better.




11 comments:
Looking at Graph 1: Hair vs. Height, we can see that as height increases, the hair length decreases in cm. There is a strong negative correlation because you can clearly see the scatter points heading down in a diagonal line. After reading the graph, I can infer that the taller students are in our classroom, the shorter their hair is in length. There are a few outliers in the graph, and if those outliers were removed, the correlation line would look stronger because all the scatter points would be close to the line of best fit.
Looking at Graph 2: Height vs. Shoe Size, we can see that as shoe size increases, the height increases as well, giving us a strong positive correlation. Shoe size might not cause height to change but height could change the shoe size because the taller a student is, it's possible that the bigger shoe size they have. Some values are common because since we are all around the same age, we follow the average statistics on our age.
Looking at Graph 3: Shoe Size vs. Hair Length, we can see that as the hair length increases, the the shoe size decreases, giving us a strong negative correlation. In my opinion, the points are not clustered in an interesting way because the data we got is what I would have predicted, (guys are taller and have shorter hair than girls who are shorter and have longer hair). A third variable that might be causing the relationship between shoe size and hair length might be the gender of the student. Correlation does NOT imply causation because their can be many other variables affecting the data to be the way it is.
Jennifer G.
Graph1 hair vs height.
There is a negative, -0.57,strong correlation.
There is a lot of outliers and it will still give us the same correlation .
Graph2 height vs shoe size
There is a positive 0.61 strong correlation. It goes either way but height kinda effects shoe sizes in this data. Same as the opposite. Shoe increase height.
Graph3 shoe size vs hair length
This shows a negative -0.82 vary strong correlation. The third variable is height but it could also be ancestors genes of how long hair you get and size feet you have also the height could be effected by parents genes. Does correlation imply caustion? Hell naww cause there can be many other variables that could cause these effects that we can't see.
Rodriguez, O
Graph 1:
strong correlation, negative. Info tells us that there is no correlation between height and hair length. There are a couple extreme points; if taken away the correlation would start leaning to a correlation of zero. Other data that would help interpret the data would be the ages of the participants.
Group 2:
strong correlation, positive. Info collected does not allow to infer causation. Although the correlation is strong, the research method doesn't let say which causes which. Some people had the same shoe sizes but the reasons are not known.
Group 3:
Correlation negative, its close to -1 so it is very strong. The clustered point tends to be related with the most seen shoe sizes. A third variable causing the results could be gender. Correlation does not imply causation. Mainly because although the info gathered shows correlation there are many variables that we don't know about that could affect the data.
Jazmin V
From the Hair Length vs Height graph, we can see that when a person is short, they have the longest hair length. We can also see that-that happens for a long time until we hit over the 165 cm of height, that is when the hair length drops more. From the graph, there is a small correlation and it is weak. The correlation is negative because as the height begins at a small centimeter measurement, the length of hair starts being long. This tells me that the students with longer hair tend to be the shortest. In the graph, it doesn’t seem as if there are many outliers because most of the points are following the path of the line. If the outliers were to disappear, I think that the graph will look the same because of the start and end points.
The Height vs Shoe Size graph shows the shoe size in a centimeter of 22 is repeated through a variety of heights. I can also suggest there is no relationship between the shoe size and the height of a person because the heights with the shoe size of 22 are increasing. To prove the point even further; the height of 167 has a shoe size that is lower than a person with a height of 170. There is a correlation, but is it weak and is positive. Shoe size and height don’t cause each other based on the graph, there would have to be more participants to further analyze and discuss whether there is a cause. Some values can be common due to human error as a possibility.
What the Shoe Size vs Hair Length graph suggests is that there is a possible relationship between them. The hair length increases, the shoe size decreases. From this, I can say that there is a correlation that is weak and is negative. The points are clustered in a way that points stay at the measurement of a 24 and 22 shoe size length while the hair length is increasing. A third variable can be whether the person has cut their hair in the duration of the last few days or weeks; this can interfere with proper data. From this graph, outliers are not visible because the points all lie within the area of the line.
Bryan M.
None of the three graphs are linear. The data is all scattered around. But there is a best fit line in all three graphs. There is no relationship between the axis in any of the three graphs. The correlation coefficient in all the graphs is below 1.
J.C
In the first correlation graph " Hair vs Height" , the best fit line indicates that the taller the students are , the shorter hair they will have . The best fit line has a negative slope which means there's a correlation. The correlation is -0.57 which tells us that the correlation is average since the closer the correlation gets to 1 or -1 indicated how strong the correlation is. Students can have a variety of hair length which has nothing to do with the height of a person which can drastically change the plots on this graph.
In the second correlation graph " Height vs Shoe Size" the correlation is positive. As height increases the students shoe size increases . The correlation coefficient is 0.61 which indicates that the correlation is mildly strong. The more taller a person does not neccesarily mean that it will have a bigger size but being taller means that you should have a bigger foot to match your size.
In the third correlation graph "Shoe Size vs. Hair Length " their is a negative correlation . The correlation coefficient is -0.82 which indicates that is a strong correlation. There is no cluster . A third variable that can be what affected this data is gender . Males tend to have bigger shoe sizes as well as be more taller than females and none of this data indicates which gender or if both genders were being used for the data . Correlation does not imply causation for the reason that a third variable can be the causation
Kevin J.
In the hair vs. height graph, there was a negative correlation that looks to be neither weak nor strong, but somewhere between the two. The graph tells me that most short haired people are tall and vise versa, but then again it doesn't make mention of gender. Correlation would become stronger if outliers were to be thrown out. In the Height vs. shoe size graph, As shoe size increases so does the length of hair - this is the relationship that can be observed. The correlation is positive and seems moderately strong. Some values are common since many people seem to have 22cm long shoes. In the graph shoe size vs. hair length, there seems to be some strong correlation between shoe size and hair length, though this is most likely due to the third hidden variable which is gender; most males have short hair but larger feet then their female counterparts.
Matt J.
From the first correlation we can draw the conclusion that the taller students have shorter hair. Since the best fit line has has a negative slope that means there is a correlation.The correlation's value is -o.57 which indicates it is average because it depends on how close a number is to 1 or -1 to say if it is strong or not.
In the second graph, the conclusion I drew from it was that as height increases, shoe size does as well. The correlation is a positive and since the coefficient is 0.61 that that indicates it is sort of strong. Shoe size does not have impact on height and height does not have an impact on shoe size however it seems that the taller you are the more likely your feet will be bigger in order to align with your height.
In the third graph, the longer the students hair the smaller their feet. There is a negative correlation in the third graph however since it has a coefficient of -0.82, that means the correlation is strong because it is closer to -1. No cluster is shown. A third variable that could be considered could be family history or gender. Correlation does not imply causation because there can be multiple factors that may not be shown in the data that impact the results.
Alex P.
The scatter plot of hair length vs. height shows that in our class the students that are shorter are the ones that have the longer hair. Much of the data shows that the hair length is decreasing when the height increases. Although the data is scattered all over the graph my inference is that in our class we have short and tall ladies and short and tall gentlemens, which means that the gender wouldn’t play a part in this graph. There is a correlation and the correlation coefficient is -0.57, I do think it is strong and negative because estimating this number to the nearest tenth will be -0.6 and any number above a 5 should be considered strong. The correlation isn’t super strong but it is strong. I do think there is a few “outliers” because there is two ladies in our class that are tall and have super long hair so I feel like the data would be more neutral if we added them. More information that I think will help interpret the data even better is if we could’ve more accurate data or at least have it make sense because i know that most of the tall people in our class have long hair.
In the shoe size vs. height graph the shoe size is constant for many heights. There is 4 rows of data that is the same for the size of shoe but not the height. The relationship I see on the graph is that the data seems to not be affected by either the shoe size or height. The most constant shoe size is 22cm for 150cm-165cm of height. There is a correlation and the correlation coefficient is 0.61. The correlation is positive and strong but not extremely strong. The shoe size causing the height to change and the height causing the shoe size to change are both invalid because neither of those factors affect the change in the graph. Most points are the same in shoe size but not height. Some values are so common because shoe sizes don’t depend on height anybody can be short or tall with a big or small foot. There is some sizes that are often the same for people of different heights for example sizes 6-7 in shoes sell out faster in store than the 8-10s.
In the shoe size vs. hair length graph there is a correlation it is negative but very strong. The points are clustered in a interesting way because the shoe sizes seem to be constant like graph 2 . The third variable that is not shown is the gender and I strongly feel that gender does affect shoe size and hair length. Correlation cannot imply causation because there is not much information given. Shoe size, hair length, and height don’t necessarily connect in the sense where there is short students with small shoe size but longer hair and there is students that are tall with less hair and a larger shoe size. Correlation doesn’t allow researchers to see the cause and effect relationships in the data.
Janet, R
The graph depicts that, the shorter the hair length, the taller the person. Yes, there is a semi-strong correlation between hair length & height. The top three tall people roughly have a hair length of: 0 cm, 10 cm, & 11cm. The top three short people have a hair length of about: 53cm, 59cm, & 60 cm. The outliers in the data are the really tall & really short people. People who seem to be of average height from the data also have average hair length. It's a negative relationship as hair length decreases while height increases.
The relationship & correlation that can be seen is that people with a 22 cm shoe size have varying heights & that as height increases, so does shoes, slowly. The varying heights start from 150 cm to 164 cm in a 22 cm shoe size. Shoe size does not cause a change in height. Height causes a change in shoe size, slowly increasing over time. It's also positive.
Yes, there's a correlation between shoe size & hair length. The smaller the shoe size, the longer the hair length. It's negative because a decrease in shoe size (y), gives an increase in hair length (x). The points on shoe size 22 are clustered in an interesting way, as they show varying lengths of hair between 25-44 cm, an increase. The variable of height may be causing the relationship between hair length & shoe size, as shoe size & height, have a similar cluster of data. The correlation does imply causation because smaller shoe sizes show that hair length is shorter.
Lizet D.
Post a Comment